HYPER-TesT
© Laurent Dubois 2001
Against pop-ups, free and really
convivial:
The Hyper-TesT, with visuo-spatial and algorithmic
subtests, is power-type IQ test intended to measure the power of reasoning and the
persistence.
A non expected but pertinent
answer will be taken into account in the raw score, and weighted according to
its degree of quality.
There is no time limit;
material help allowed: books, calculator, computer, internet…, corrections and
additions are not accepted; no discussion with others, no help from anyone in
any way.
Requisites : logic,
imagination, shrewdness, minimal general knowledge, and a very very good sense
of observation. Send your answers to 916test@caramail.com
Or to the following address:
Laurent Dubois, rue Beaulieusart, 148, Fontaine-L’Evêque, 6140, Belgium.
Please include your name,
age, gender, e-mail address, and native language. If relevant, please list
scores on previously-taken IQ tests, along with the names of the tests.
It’s important to normalize the “Hyper-TesT”. Thanks for your comprehension.
The Hyper-TesT is an
admission test for the SIGMA
Society and potentially for several other societies (Cerebrals, Glia, Poetic
Genius, Pi, Mega…).
See the PROJECTED NORMS.
See the SCORING SCALE.
The correction is free!

Read carefully the following
warning !
WARNING
You have to choose the most
basic, the most general and the most precise solution. To avoid confusion,
don’t “point out” the solution; write or draw it completely! If there is the
most little part of subjectivity or interpretation in your answer, this is not
the good answer!
A potentially infinite series is indicated by the
dots; the hyphens indicate the number of elements (not asked) after the
question mark; otherwise, there is logically nothing else possible after the
last element.
The numbering of the items
doesn’t belong to the items!
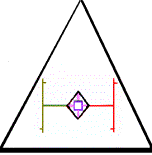
Principle of an analogy:
“black : white :: true : false” must be read as this: white is to black as
false is to true.
The analogy Part
: Part : Part : Part : (...) :: Whole : ? is
the generic item in each part of the Power-scale.
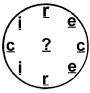
1) What time is it ?
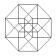
2) Which is the odd one
out?
![]()
![]()
![]()

a b c d e
3) Which two of the following figures do not belong
to the same family as the three others?

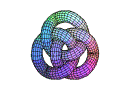
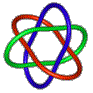

a b c d e
4) analogy
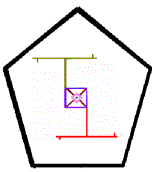 :
: 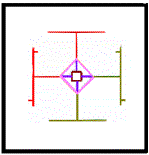 ::
::  : ?
: ?
 5) The square of squares
5) The square of squares
Here is a square constituted by 4 small squares.
Having known that figures 1 , 2 , 3 or 4 should be distributed at random each
in one of four small squares, and that every small square can be put in
rotation of 90 °, 180° or 270°, how many different configurations are
possible, in other words, how many big different squares as it is could obtain?
6) The "Fractal
Chessboard"

You have a
normal chessboard. You keep a version of that chessboard - we call it
chessboard A; you make 32 scale models of that chessboard, named chessboards A'
so as to replace the 32 white cases of chessboard A by the 32 scale model A'.
Therefore, you have a new chessboard with 32 black cases and 32 chessboards A'. We'll name it chessboard
B. You keep a version of that chessboard B. After that, you make 32 scale
models of that chessboard, named chessboards B' so as to replace the 32 black
cases of chessboard B by the 32 scale model B'. Therefore, you have a new
chessboard with 32 chessboards B' cases and
32 chessboards A' cases. We'll name it chessboard C. You keep 2 versions of that chessboard C;
you make 64 scale models of that chessboard, named chessboards C' so as to
replace the 32 white cases of chessboard C (i.e. cases corresponding to white
cases on initial chessboard A) by 32
scale model C'; this new chessboard is named C1. You take now your second
version of chessboard C and you replace
the 32 black cases of that second chessboard C (i.e. cases corresponding to
black cases on initial chessboard A) by the last 32 scale model C'; this new
chessboard is named C2.
You compute
how many self-coloured black and white cases
each chessboard C1 and C2 contain? Then you make "number cases
chessboard C1 minus number cases chessboard C2". You have a number. We
call this number N.
The
question is: what is the square root of the number you obtain when you add the
smallest possible square number to the number N necessary to have another
square?
7) the marvellous motive
which is the correct figure to complete the
motive?

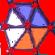
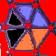
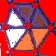
a b
c d e f
g h
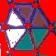
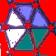
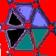
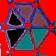
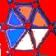
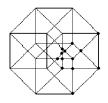
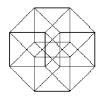
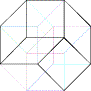
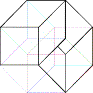
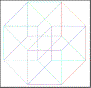
8) The Hypercube’s Declination
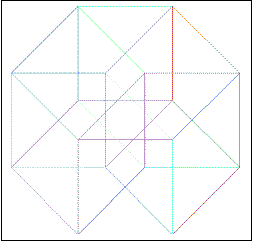
a) Is it possible to draw a tesseract with an unique broken line? (you
cannot lift up the pencil nor retrace yours's steps) If yes, number the lines
b) How many distinct regular volumes can you clearly detect in this
“representation” of an Hypercube?
c) Three dices joined side by side in an Hypercube. One face is
given: face one.
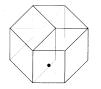
The
question is: how much configurations are possible with the 6 different values?
Please, draw them.
d) Complete the last figure
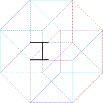
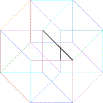
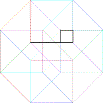
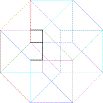
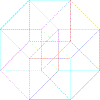
e) Add the missing point in the last figure
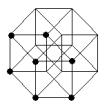
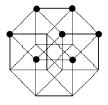
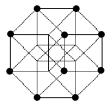
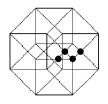
f) Complete the last figure algo
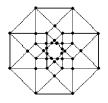
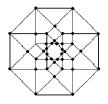
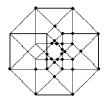
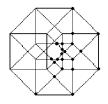
g)
 :
:
 ::
::
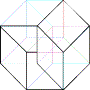 : ?
: ? 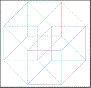
h)
 :
:
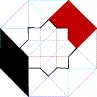 ::
::
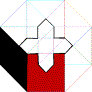 :
?
:
?
i) What is the missing number? (the smallest number, viewed with
difficulty, is 24)
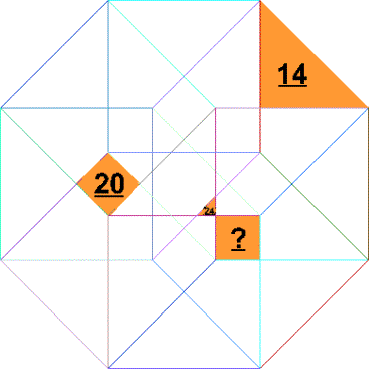
j) What is the maximum number of
completely bounded volumes that can be formed by all the interpenetrating
regular volumes of this “representation” of an Hypercube, considering only the
surfaces of the volumes as bounds and counting only volumes that are not
further subdivided? Prove your answer.
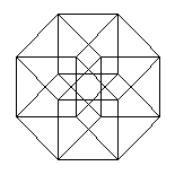
k) The Hypercube’s Labyrinth
------------------------------
Which is the missing line?
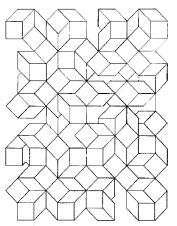
9) The moebius Chessboard
 a) Find the number of non-attacking
queens necessary to cover a mobius strip chess-board of 64 squares and prove
that this number is minimal.
a) Find the number of non-attacking
queens necessary to cover a mobius strip chess-board of 64 squares and prove
that this number is minimal.
b) Find the maximal number of non-attacking queens necessary to cover a
mobius strip chess-board of 64 squares.
10) The Magic Puzzle
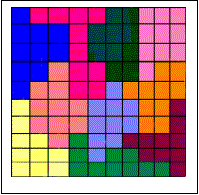
You can
solve the problem on the following page :
http://www.fitzweb.com/brainteasers/puzzlers.shtml
Don’t
forget to write your name in the appropriate field.
 11) Knight’s tour
11) Knight’s tour
The
objective of this puzzle is to pass all the squares of the board with the
knight, making only legal moves. A legal move for the knight is shaped like an
L. Up or down two squares and over one square. The knight starts in a random position.
Click on the square that you want to reach from there. It will be occupied by a
new piece. Continue until the whole board is filled.
solve the
puzzle at the following adress and print your solution
http://enchantedmind.com/puzzles/knights/knight.html
12) Sphere


13) Which is the
following figure?
![]()
![]()
![]()
![]() ?
?
![]()
14) Abyss
Part : Part: Part: Part:(...) :: Whole : ?
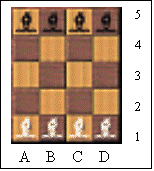
15) The Bishops’s Conversion
5 The goal
is to move all the white bishops to the top and all the black bishops to the
bottom
Alternate moves
- white moves first, then black, then white, etc.
You can't
place a bishop on a square where it can be captured by an opposing bishop
You may
only make valid chess bishop moves (diagonal only and as many available squares
as one wants in the chosen direction)
You can solve the problem on the
following page :
http://www.chez.com/remuemeninges/bishex.htm or
http://www.chesscorner.com/fun/gentlebishops/bishops.html (don’t forget to note your moves)
Don’t forget to write your name in the
appropriate field. WARNING: Please note your moves as there are problems with the all of fame page. Sorry for the inconvenience.
916 TesT Concep-T Power-Scale
ÓNEUROLAND2000Ò
|
|
|
|
|
|