HYPER-TesT
© Laurent Dubois 2001
Against pop-ups, free and really
convivial:
L’Hyper-TesT, avec ses items
“visuo-spatiaux” et “algorithmiques”, est un test de Q.I. destiné plus
spécifiquement à évaluer la puissance et la persistence du raisonnement.
La soumission d’une réponse non prévue mais pertinente donne
droit à une gratification dans le score brut à hauteur de la qualité de cette
réponse.
Il n’y a pas de limite de temps. Toutes les références possibles
(encyclopédies, calculatrice, Internet…) sont permises ; corrections et
additions ne sont pas acceptées ; aucune demande d’aide d’aucune sorte à
quiconque et d’aucune façon n’est autorisée.
Requis : logique, imagination, finesse, très peu de connaissances,
un grand sens de l’observation.
Envoyez vos réponses à 916test@caramail.com ou à l’adresse suivante :
Laurent Dubois, rue Beaulieusart, 148, Fontaine-L’Evêque,
6140, Belgique.
Merci d’indiquer vos nom, âge, sexe, langue et adresse
email, et éventuellement vos résultats aux tests de QI que vous avez déjà
passés ainsi que le nom des tests. Ceci est indispensable pour la normalisation
du « test 916 ». Merci de votre compréhension.
L’Hyper-TesT est un
test d’ admission à la société SIGMA et potentiellement à d’autres sociétiés (Cerebrals, Glia,
Poetic Genius, Pi, Mega…).
Cfr. PROJECTED NORMS
Cfr. SCORING SCALE
La correction est gratuite.

Lisez attentivement l’avertissement suivant !
AVERTISSEMENT
Vous
devez choisir la solution la plus simple, la plus générale et la plus précise.
Pour éviter toute confusion, n’indiquez pas la réponse, écrivez-la ou
dessinez-la complètement ! s’il y a la plus petite part de subjectivité ou
d’interprétation dans votre réponse, c’est qu’elle n’est pas correcte.
Les
points de suspension indiquent qu’une série est potentiellement infinie ;
les tirets indiquent le nombre d’éléments (non demandés) qui viennent après le
point d’interrogation ; sans autre indication, rien ne peut logiquement
venir après la dernière figure.
La
numérotation des items ne fait pas partie des items!
Principe
d’une analogie: “blanc : noir :: faux : vrai” doit être lu comme suit: noir est
à blanc comme vrai est à faux
L’analogie
Partie : Partie : Partie : Partie : (...) :: Tout : ? est
l’item générique dans chaque partie de l’Echelle de Puissance.
D.
1) quelle heure est-il?
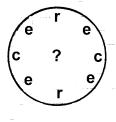
2) quelle figure
faut-il exclure?
![]()

![]()

a b c d e
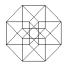
3) quels sont les deux
éléments de cette série qui ne font pas partie de la même famille?
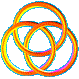

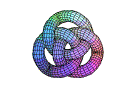


a b c d e
4)
Analogie
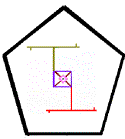 :
: 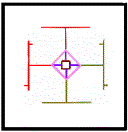 ::
:: 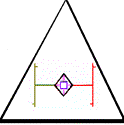 : ?
: ?
 5) le carré de carrés
5) le carré de carrés
Voici un carré
constitué de 4 petits carrés. Sachant que les chiffres 1 , 2 , 3 or 4 peuvent
se trouver au hazard chacun dans un petit carré différent, et que chaque petit carré
peut effectuer une rotation de 90, 180 ou 270, degrés, combien de
configurations différentes sont possible,
en d’autres mots, combien de grands carrés différents peut-on
obtenir ?
6) L’échiquier fractal
 Vous avez un échiquier normal. Vous gardez
une version de cet échiquier - nous l'appelons l'échiquier A; vous faites 32
modèles réduits de cet échiquier, appelés échiquiers A' de façon à remplacer les
32 cases blanches de l‘échiquier A par les 32 modèles réduits A'. Par
conséquent, vous avez un nouvel échiquier avec 32 cases noires et 32 modèles réduits A' à la place des cases
blanches. Nous appellerons cet échiquier B. Vous gardez une version de cet
échiquier B. Ensuite, , vous faites 32 modèles réduits de cet échiquier B,
appelés échiquiers B' de façon à remplacer les 32 cases noires de l‘échiquier B
par les 32 modèles réduits B’. Par conséquent, vous avez un nouvel échiquier
avec 32 échiquiers B' à la place des cases noires et 32 échiquiers A' à la place des cases blanches. Nous appellerons
cet échiquier C. Vous gardez 2 versions
de cet échiquier C; vous faites 64 modèles réduits de cet échiquier, appelés
échiquiers C' de façon à remplacer les 32 cases blanches de l‘échiquier C (i.e.
les cases correspondant aux cases blanches sur l’échiquier initial A) par 32
modèles réduits C'; ce nouvel échiquier est appelé C1. Vous prenez maintenant
votre seconde version de l’échiquier C et vous remplacez les 32 cases noires de
ce second échiquier C (i.e. les cases correspondant aux cases noires sur
l’échiquier initial A) par les 32 modèles réduits C' qu’il vous reste; ce
nouvel échiquier est appelé C2.
Vous avez un échiquier normal. Vous gardez
une version de cet échiquier - nous l'appelons l'échiquier A; vous faites 32
modèles réduits de cet échiquier, appelés échiquiers A' de façon à remplacer les
32 cases blanches de l‘échiquier A par les 32 modèles réduits A'. Par
conséquent, vous avez un nouvel échiquier avec 32 cases noires et 32 modèles réduits A' à la place des cases
blanches. Nous appellerons cet échiquier B. Vous gardez une version de cet
échiquier B. Ensuite, , vous faites 32 modèles réduits de cet échiquier B,
appelés échiquiers B' de façon à remplacer les 32 cases noires de l‘échiquier B
par les 32 modèles réduits B’. Par conséquent, vous avez un nouvel échiquier
avec 32 échiquiers B' à la place des cases noires et 32 échiquiers A' à la place des cases blanches. Nous appellerons
cet échiquier C. Vous gardez 2 versions
de cet échiquier C; vous faites 64 modèles réduits de cet échiquier, appelés
échiquiers C' de façon à remplacer les 32 cases blanches de l‘échiquier C (i.e.
les cases correspondant aux cases blanches sur l’échiquier initial A) par 32
modèles réduits C'; ce nouvel échiquier est appelé C1. Vous prenez maintenant
votre seconde version de l’échiquier C et vous remplacez les 32 cases noires de
ce second échiquier C (i.e. les cases correspondant aux cases noires sur
l’échiquier initial A) par les 32 modèles réduits C' qu’il vous reste; ce
nouvel échiquier est appelé C2.
Vous comptez combine de cases unies noires et blanches contient chacun de ces échiquiers C1 and C2. Vous soustrayez le nombre total de cases de C2 de C1 ; vous obtenez un nombre N.
La question est: Quelle est la racine carrée du nombre que vous obtenez en ajoutant le plus petit carré possible à N pour obtenir un autre carré ?
7)
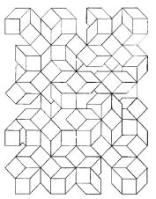
Le
merveilleux motif
Compléter cette figure?

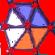
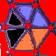
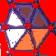
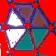
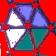
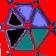
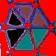

a b c d e f g h
8)
les Déclinaisons de l’hypercube
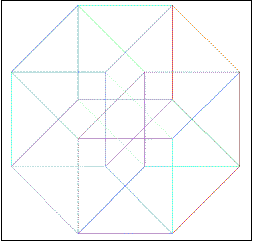
a) Combien de traits pouvez-vous tracer sans lever le crayon?
b) Combien de volumes réguliers distincts pouvez-vous détecter dans cette « représentation » d’un Hypercube?
c) Trois dés joints dans un Hypercube. Une face est donnée: une face 1 .
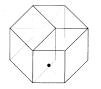
La question est: combien de configurations différentes sont possible? Dessinez-les.
d) Compléter la dernière figure
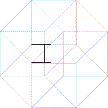
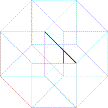
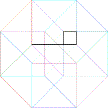
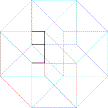
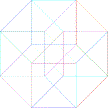
e) Ajouter le point manquant dans la dernière figure
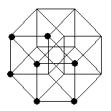
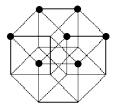
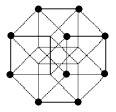
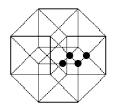
f) Compléter la dernière figure
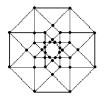
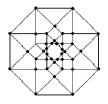
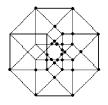
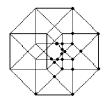
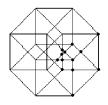
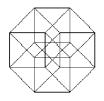
analogies
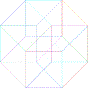
g)
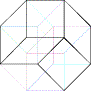 :
: 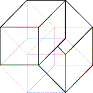 ::
:: 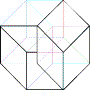 :
?
:
? 
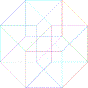
h)
 :
: 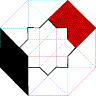 ::
:: 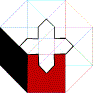 : ?
: ? 
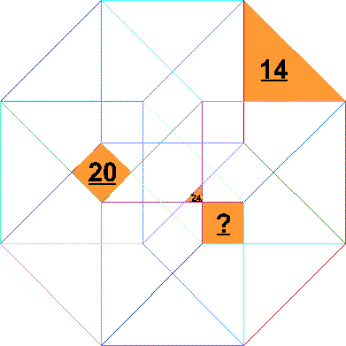
i) Quel est le nombre manquant? (le plus petit nombre, vu avec difficulté, est 24)
j) Quel est le nombre maximum de volumes complètement limités qui peuvent être formés à partir des volumes réguliers qui s’interpénètrent dans cette « représentation » d’un hypercube? Les limites sont constituées par les surfaces des volumes réguliers et on ne tiendra compte que des volumes qui ne sont pas subdivisés. Prouvez votre réponse.
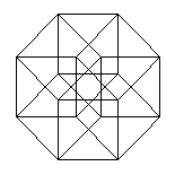
k) le
Labyrinthe d’Hypercubes
------------------------------
Quelle est la ligne manquante?
9) l’échiquier de möbius
 a)
Trouver le nombre de reines non en prise nécessaire pour couvrir un échiquier
de Möbius de 64 cases et prouver que ce nombre est minimal.
a)
Trouver le nombre de reines non en prise nécessaire pour couvrir un échiquier
de Möbius de 64 cases et prouver que ce nombre est minimal.
b) Trouver le nombre de reines non en prise nécessaire pour couvrir un échiquier de Möbius de 64 cases et prouver que ce nombre est maximal.
10) le Puzzle Magique
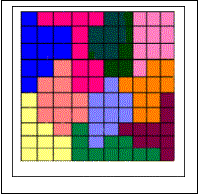
Vous pouvez résoudre le problème à la page suivante :
http://www.fitzweb.com/brainteasers/index.html
N’oubliez pas d’inscrire votre nom dans le champ approprié.
11)  Knight’s
tour
Knight’s
tour
L'objectif de ce problème est de passer par toutes les cases de l’échiquier avec le cavalier, en faisant uniquement des coups légaux. Un mouvement légal pour le chevalier a la forme d’un L : d’abord deux cases verticalement ou horizontalement, puis une case perpendiculaire. Le cavalier commence dans une position aléatoire. Effectuez un clic sur la position que vous voulez atteindre. Il sera occupé par un nouveau morceau. Continuez jusqu'a ce que l’échiquier entier soit rempli.
Résolvez l'énigme à l'adresse suivante et imprimez votre solution
http://enchantedmind.com/puzzles/knights/knight.html
12) Sphère


13) Quelle est la grille suivante?
![]()
![]()
![]()
![]()
14) abysses
Partie : Partie : Partie : Partie : (...) :: Tout : ?******
15) L’échange de fous
Le but est d’inverser les positions des fous blancs et noirs.
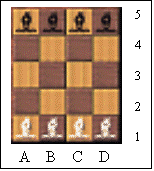 Coups
alternés: coup blanc, coup noir, coup blanc, etc.
Coups
alternés: coup blanc, coup noir, coup blanc, etc.
Vous ne pouvez placer un fou sur une case accessible par un fou de la couleur opposée
Vous devez respecter le mouvement légal des fous aux échecs (déplacement diagonal uniquement et d’autant de cases libres disponibles dans la direction choisie qu’on le souhaite)
Vous pouvez résoudre le problème à la page suivante :
http://www.chez.com/remuemeninges/bishex.htm (N’oubliez pas d’inscrire votre nom dans le champ approprié. ATTENTION: veuillez noter vos coups; il y a des problèmes avec la page Hall of fame. Désolé pour les inconvénients.) ou
http://www.chesscorner.com/fun/gentlebishops/bishops.html (n’oubliez pas de noter vos coups. )
ÓNEUROLAND2000Ò
